В этом уроке я расскажу про функция стандартного отклонения. И покажу на конкретном примере, зачем она нужна, как ее можно использовать при анализе данных и как она выглядит в DataLens.
Зачастую для сложного анализа данных простых функций и инструментов недостаточно. И приходится прибегать к использованию сложных статистических функций. В некоторых случаях они очень могут помочь. И начнем серию выпусков про такие сложные функции со стандартного отклонения.
Стандартное отклонение: определение, применение и важность
Стандартное отклонение (SD) является одним из наиболее важных статистических инструментов, используемых для измерения разброса и вариабельности данных. Это показатель того, насколько значения в наборе данных отличаются от среднего значения. В данной статье мы рассмотрим определение, применение, и важность стандартного отклонения.
Определение
Стандартное отклонение представляет собой меру степени разброса данных вокруг среднего значения. Оно показывает, насколько значения отклоняются от среднего значения, и позволяет оценить, насколько данные однородны. Стандартное отклонение рассчитывается по формуле:
где x̅ - среднее значение набора данных, а x - каждое отдельное значение в наборе.Применение
Стандартное отклонение используется в различных областях, включая финансы, экономику, статистику и многие другие. Вот несколько примеров его применения:
- Анализ рисков: Стандартное отклонение является ключевым инструментом при оценке рисков в финансах. Чем выше стандартное отклонение, тем выше риск, связанный с инвестициями или портфелем.
- Оценка эффективности: В экономике стандартное отклонение используется для сравнения эффективности различных компаний или отраслей. Чем ниже стандартное отклонение, тем более стабильной и предсказуемой является компания или отрасль.
- Прогнозирование: В статистике стандартное отклонение используется при построении прогнозов. Если данные имеют высокое стандартное отклонение, то прогнозы будут менее точными.
Важность
Стандартное отклонение имеет важное значение в различных областях по следующим причинам:
- Измерение риска: Как уже упоминалось, стандартное отклонение является ключевым показателем при анализе рисков. Чем выше его значение, тем выше степень риска.
- Прогнозирование и управление рисками: Прогнозы и оценка рисков становятся более точными и надежными при использовании стандартного отклонения в качестве меры разброса данных.
Заключение
Стандартное отклонение является важным статистическим инструментом, который позволяет измерить разброс данных и оценить степень их вариабельности. Оно имеет широкое применение в различных областях и служит ключевым показателем при оценке рисков и прогнозировании. Правильное использование стандартного отклонения может значительно улучшить качество анализа данных и принятия решений.
Практическое применение
А теперь давайте посмотрим, как именно выглядит это на практике. На самом деле, все намного проще и понятнее. Давайте смоделируем две ситуации и попробуем их проанализировать.
Представим, что в ситуации 1 у нас будет одна величина. Это могут быть продажи, расходы, неважно. А в ситуации 2 другая величина.
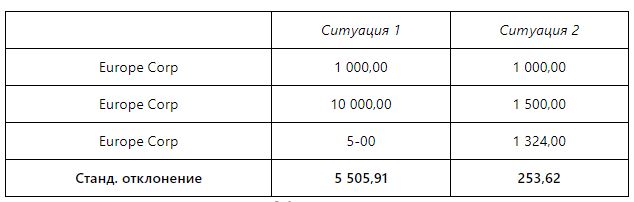
Так вот, стандартное отклонение показывает разброс этих самых величин от средней. Очевидно, что в ситуации 1 суммы очень разные, а в ситуации 2 примерно одинаковые и разброс минимален.
В одном источнике мне попался еще один очень наглядный пример с зарплатой. Допустим, вы собираетесь устроится на работу, где средний уровень дохода 70 т.р., а стандратное отклонение 10 т.р. В данном случае оно нам подскажет, что в данном месте вы сможете рассчитывать как минимум на зарплату в 60 т.р. То есть ваша зарплата будет около 70 т.р., плюс минус 10 т.р.
А вот если бы отклонение было 50 т.р., то тут спрогнозировать свою зарплату было бы сложнее. Плюс минус 50 т.р.
Вывод
Таким образом, если говорить простым языком, стандартное отклонение это аналог привычного нам понятия плюс/минус. Оно помогает понять уровень разброса данных и спрогнозировать показатели.
А как именно сделать это в DataLens, смотрите в подробном видеоуроке ниже.
Наши курсы
Видео версию данного урока можно посмотреть тут.
Если вам понравился урок, то можете поддержать проект по кнопке ниже. Это очень поможет делать для вас больше интересных и полезных выпусков. Спасибо!

Задать вопросы и обсудить волнующие темы про аналитику данных теперь можно на нашем форуме.
Если вам понравился урок, подписывайтесь на канал или группу и ставьте лайки. А также пишите в комментариях свои кейсы или вопросы. Самые интересные мы обязательно разберем.







